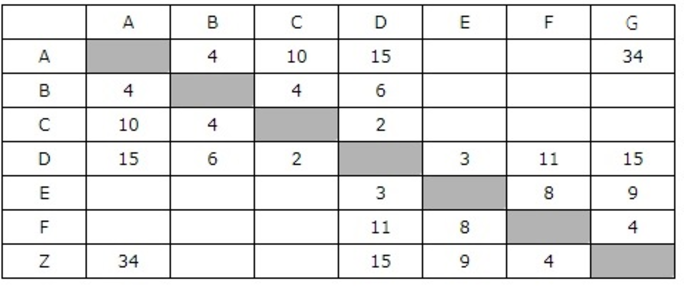
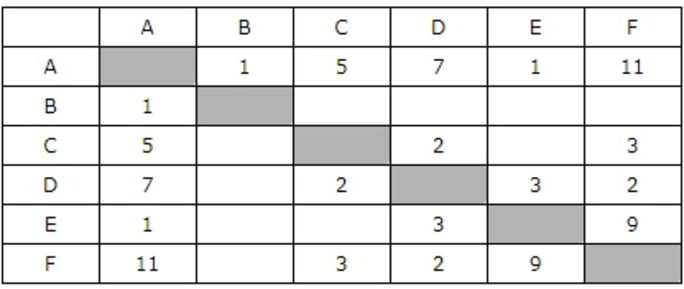
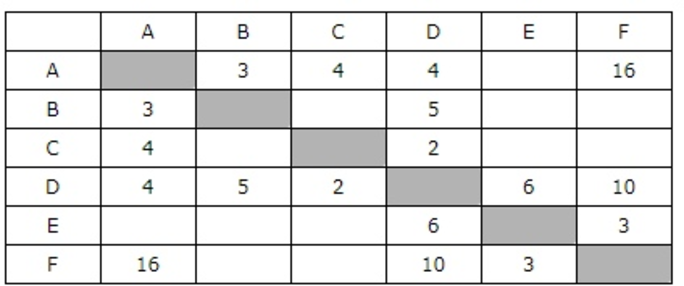
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
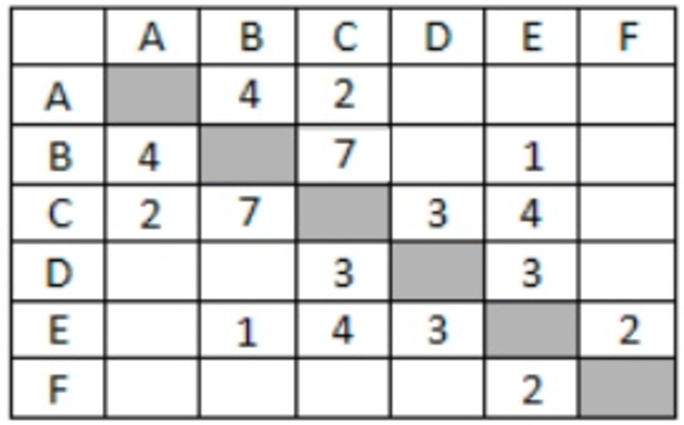
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
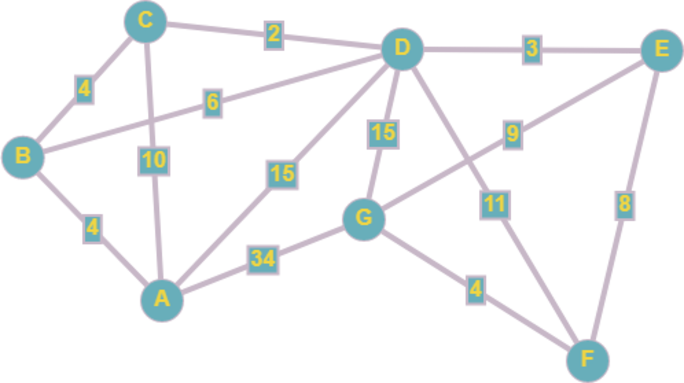
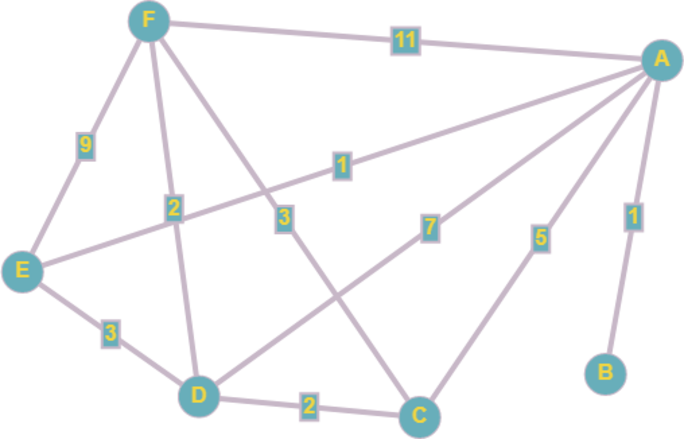
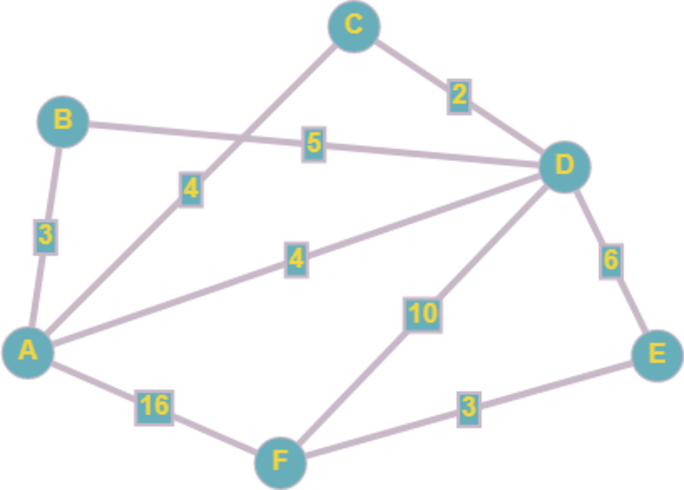
Для удобства представим таблицу в виде графа:
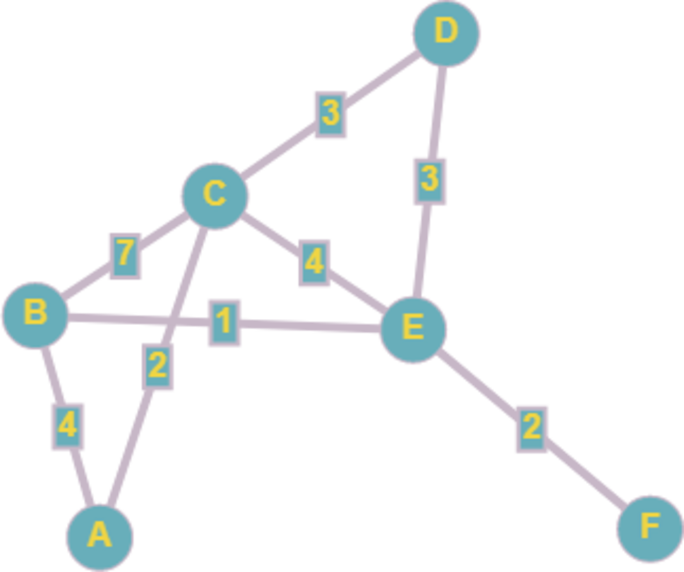
Т.к. в пункт F можем попасть только из E, сейчас задача сводится к нахождению кратчайшего расстояния между А и Е.
Сейчас нужно аккуратно разобрать все случаи. Итак, если мы идем из А в В, до Е мы можем добраться следующими способами: A-B-E = 4 + 1 = 5, A-B-C-E = 4 + 7 + 4 = 15 – причем из графа видно, что в вершину D заходить не стоит: мы сделаем крюк.
Если мы идем из А в С, то до Е мы доходим так: А-С-Е = 2 + 4 = 6. Видим, что из А до Е наименьшее расстояние по маршруту A-B-E = 5. Тогда A-F = 5 + 2 = 7.
Ответ: 7