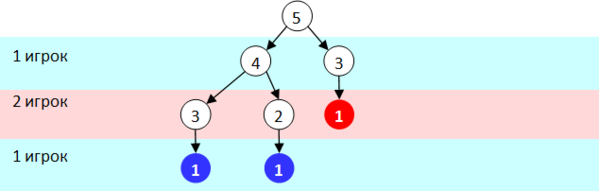
Простейшая выигрышная позиция для того игрока, кто ее создал: это 1 и 1. Понятно, что в этом случае побеждает тот, кто ходит вторым, так как у первого игрока нет хода.
Очевидно, что позиция 2 и 1 выигрышная для первого и проигрышная для второго.
Если 3 и 1, тогда второй вновь с победой, как несложно убедиться простой проверкой, так как есть ровно два хода.
Когда в кучках 3 и 2, победа у первого (убираем 3, делим 2).
Если же 3 и 3, тогда победа вновь возвращается ко второму, что можно показать простым перебором.
Замечаем закономерность: если в каждой из кучек по нечетному числу конфет, тогда позиция выигрышная для второго.
Если же хотя бы в одной из кучек четное число конфет, то такая позиция выигрышная для первого.
Несложно понять, что когда в обеих кучках по нечетному числу конфет, то за один ход нельзя получить такую же позицию, так как при разделении любого нечетного числа на два слагаемых одно из них будет четным. Однако если хотя бы в одной из кучек четное (ненулевое) число конфет, то ее несложно разбить на два нечетных слагаемых. Таким образом мы можем разбить все позиции на выигрышные и проигрышные с учетом того, сколько конфет в кучках. И задача выигрывающего делать ход на выигрышные позиции.
После этого уже понятно, кто выиграет в данной по условию игре и как ему этого добиться.
Делим все возможные ходы на «выигрышные» и «проигрышные». Если после разбиения получились две кучки с нечетным числом конфет, тогда назовем такую позицию «выигрышной», а все остальные — «проигрышные».
Стратегия победителя заключается в том, что он делает ход на «выигрышные» поля. Так как первый может сделать ход на «выигрышное» поле, а хода с одного «выигрышного» поля на другое нет, и с любого «проигрышного» поля за один ход можно попасть на «выигрышное», то побеждает начинающий. Своим первым ходом он может съест кучку из 21 конфеты, а кучу с 20 конфетами разделить на две, в которых нечетное количество конфет в обеих кучках (например, 19 и 1). Заметим, что последняя позиция, когда две кучки, по одной конфете в каждой, выигрышная, т. е. последний ход сделает первый.
Ответ: Первый игрок.