Сколько существует различных наборов значений \(x_1, x_2, ... x_{10}\), которые удовлетворяют всем перечисленным ниже условиям?
\((x_1 \wedge x_2) \rightarrow (x_3 \wedge x_4)=1\)
\((x_3 \wedge x_4) \rightarrow (x_5 \wedge x_6)=1\)
\((x_5 \wedge x_6) \rightarrow (x_7 \wedge x_8)=1\)
\((x_7 \wedge x_8) \rightarrow (x_9 \wedge x_{10})=1\)
В ответе не нужно перечислять все различные наборы значений переменных \(x_1, x_2, ... x_{10}\), при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Внешняя операция в отдельно взятом уравнении — это импликация, в результате которой должна быть истина. Импликация будет истинна, если:
\(0 \rightarrow 1\)
\(0 \rightarrow 0\)
\(1 \rightarrow 1\)
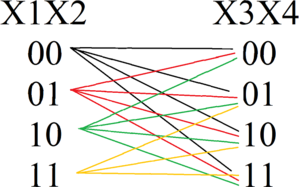
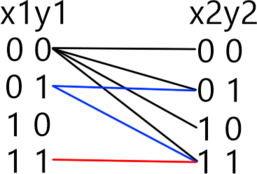
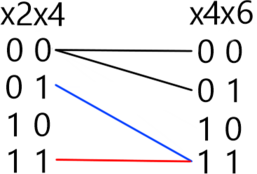
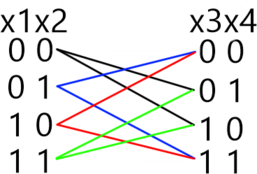
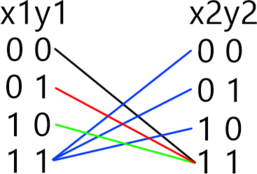
Если скобка \((x_1 \wedge x_2)=1\) \((x_1=1 , x_2=1)\), то для скобки \((x_3 \wedge x_4)\) возможен только вариант \((x_3=1, x_4=1)\), при любых других конъюнкция будет равна 0.
Если \((x_1 \wedge x_2)=0\) (это возможно в следующих случаях \(x_1=0, x_2=1; x_1=1, x_2=0; x_1=0, x_2=0)\), то для скобки \((x_3 \wedge x_4)\) возможны любые значения, импликация этих скобок будет истинна. Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на единицу, то будем использовать метод отображения, применяя его к каждой последующей комбинации \(x_{i},x_{i+1}, i \in [1; 9]\).
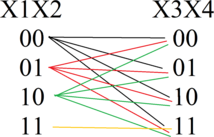
Теперь найдем общее количество решений, подставляя в отображении соответствующие x, учитывая предыдущие значения:
\(\begin{array}{|c|c|c|c|c|c|} \hline & x_1 \wedge x_2 & x_3 \wedge x_4 & x_5 \wedge x_6 & x_7 \wedge x_8 & x_9 \wedge x_{10}\\ \hline 00 & 1 & 3 & 9 & 27 & 81\\ \hline 01 & 1 & 3 & 9 & 27 & 81\\ \hline 10 & 1 & 3 & 9 & 27 & 81\\ \hline 11 & 1 & 4 & 13 & 40 & 121\\ \hline \end{array}\)
\(\begin{array}{|c|c|c|c|c|c|} \hline & x_1 \wedge x_2 & x_3 \wedge x_4 & x_5 \wedge x_6 & x_7 \wedge x_8 & x_9 \wedge x_{10}\\ \hline 00 & 1 & 1+1+1 & 3+3+3 & 9+9+9 & 27+27+27\\ \hline 01 & 1 & 1+1+1 & 3+3+3 & 9+9+9 & 27+27+27 \\ \hline 10 & 1 & 1+1+1 & 3+3+3 & 9+9+9 & 27+27+27\\ \hline 11 & 1 & 1+1+1+1 & 3+3+3+4 & 9+9+9+13 & 27+27+27+40\\ \hline \end{array}\)
В итоге получаем: \(81+81+81+121=364\).
Ответ: 364