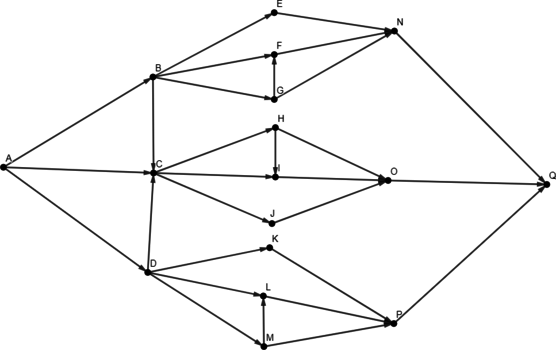
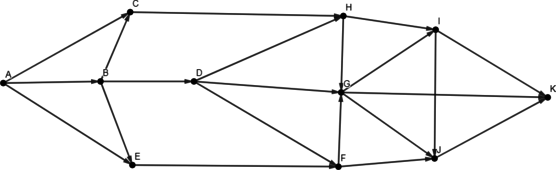
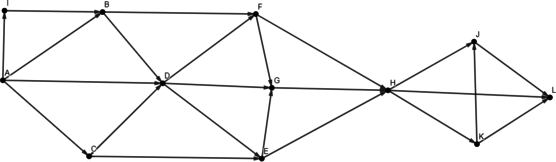
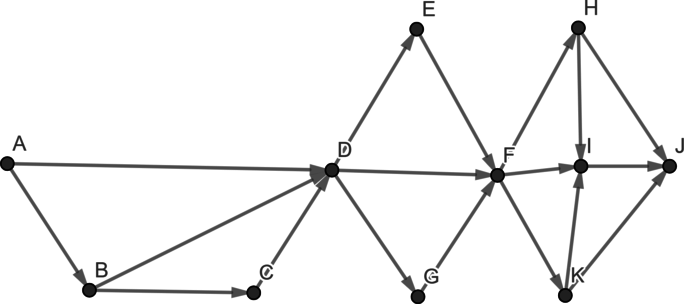
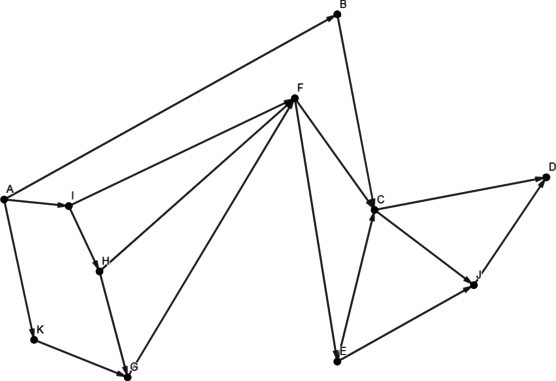
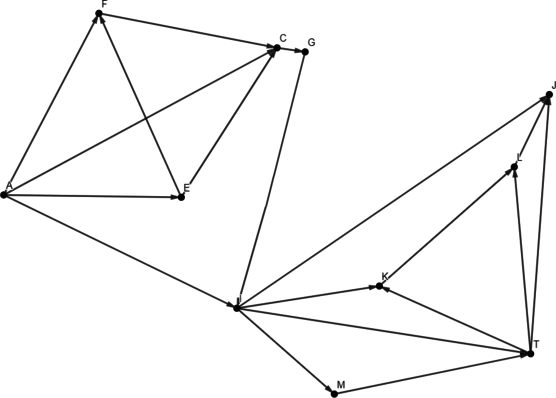
На рисунке представлена схема дорог, связывающих города A, B, C, D, E, F, G, H, I. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города A в город I, не проходящих через город E?
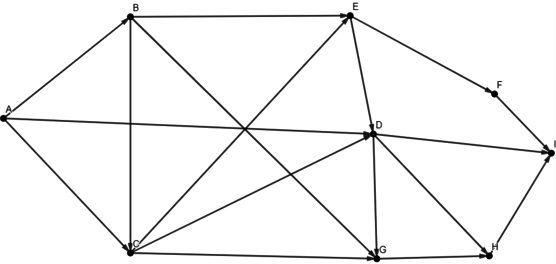
Решать будем динамикой.
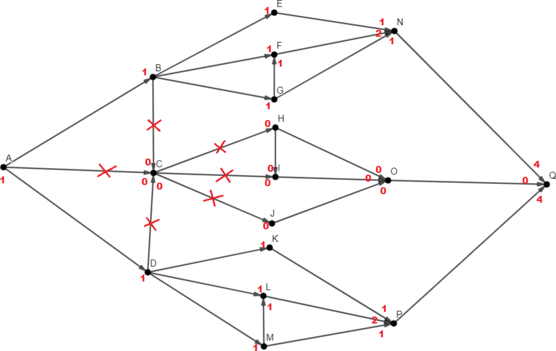
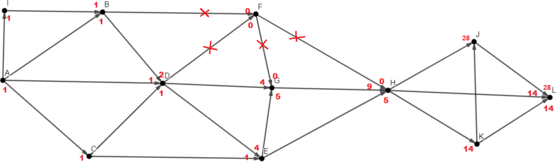
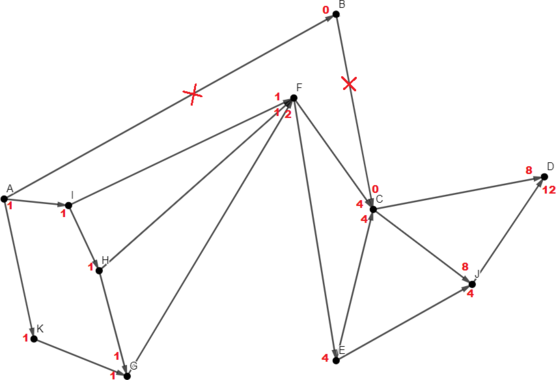
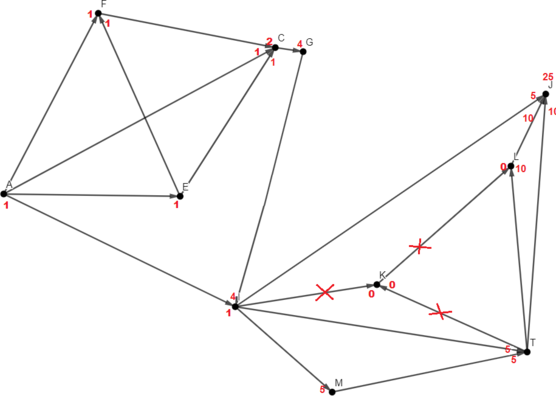
Зачеркнём те дороги, по которым нам двигаться нельзя. (Те, которые идут в город E или выходят из него)
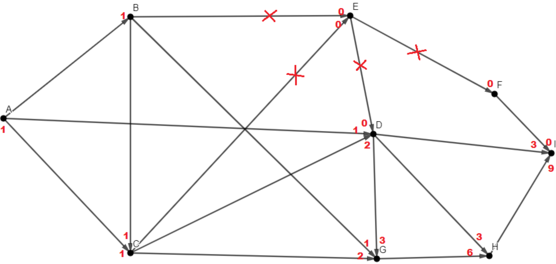
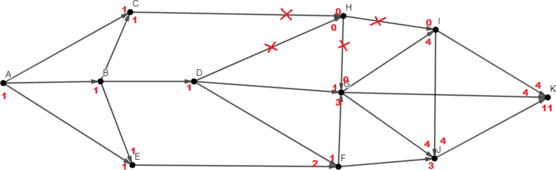
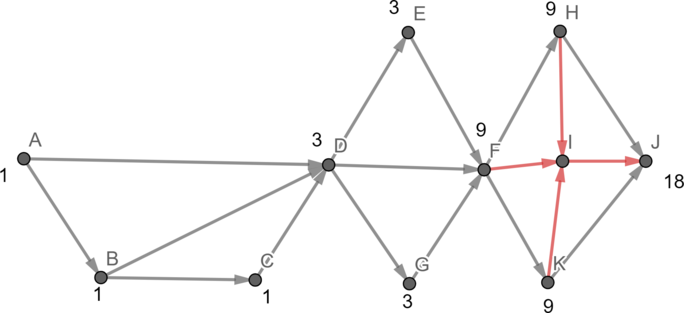
Красным отмечено, сколько путей идёт в конкретную вершину по конкретной стрелке. Заметим, что если в город идёт более, чем одна дорога, значит количество путей в этот город будет равно сумме количеств путей, ведущих в города, из которых эти дороги начинаются. В этом и есть принцип динамического решения. Получается, если сложить все красные числа, нарисованные около конкретного города, как раз можно получить количество различных путей, ведущих в этот город.
Если по дороге двигаться запрещено, количество путей, проходящих через неё равно нулю.
Нужно понимать, что в город A можно попасть одним путём: собственно, никуда не уходить из города A.
Итого получается, что в пункт I ведут 12 различных путей.
Ответ: 12