Сколько нулей в троичной записи числа \((507_8-13_{16})\cdot11_{7}\)?
Вычислим значение данного выражения в десятичной системе счисления. Для этого сначала переведём все числа, входящие в выражение в десятичную систему счисления:
\(507_8=327\)
\(13_16=19\)
\(11_7=8\)
Таким образом, исходное выражение превращается в: \((507_8-13_{16})\cdot11_{7}=(327-19)\cdot8=308\cdot8=2464\). Переведём полученное десятичное число в троичную систему счисления: \(2464_{10}=10101021_3\). Количество нулей в троичной записи получившегося числа равно трём.
Ответ: 3



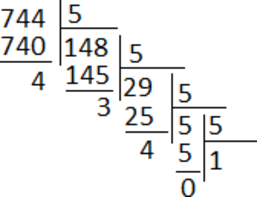 Получаем число
Получаем число 