Другие системы счисления (страница 2)

Переведём данную сумму в удобную форму для основания 4 нашей системы счисления:
\[2^{43}+2^{14}+2\] \[2^1\cdot2^{42}+2^{2\cdot7}+2\] \[2\cdot2^{2\cdot21}+(2^2)^7+2\] \[2\cdot(2^2)^{21}+4^7+2\] \[2\cdot4^{21}+1\cdot4^7+2\cdot4^0\] Соответственно, число имеет вид \(200..010..02_4\), где 2 стоит в первом разряде, 1 стоит в восьмом разряде, и 2 стоит в 22 разряде. Таким образом, ровно три цифры отличны от нуля в четверичной записи данного числа.

Ответ: 3

Переведём данную сумму в удобную форму для основания 8 нашей системы счисления:
\[2^{100}+2^{48}+2^{32}+2^{13}+2^7+2+1\] \[2\cdot2^{99}+2^{48}+4\cdot2^{30}+2\cdot2^{12}+2\cdot2^6+3\] \[2\cdot(2^3)^{33}+(2^3)^{16}+4\cdot(2^3)^{10}+2\cdot(2^3)^{4}+2\cdot(2^3)^2+3\cdot(2^3)^0\] \[2\cdot8^{33}+1\cdot8^{16}+4\cdot8^{10}+2\cdot8^{4}+2\cdot8^2+3\cdot8^0\] Соответственно, число имеет вид \(200..010..040..020203_8\), где 3 стоит в первом разряде, 2 стоит в третьем разряде, 2 стоит в пятом разряде, 4 стоит в 11 разряде, 1 стоит в 17 разряде, 2 стоит в 34 разряде. Таким образом, ровно 6 цифр отличны от нуля в восьмеричной записи данного числа.

Ответ: 6

Переведем двумя способами: 1) используя триады и тетрады и 2) через десятичную систему счисления.

1) Вспомним таблицу тетрад и триад:

Переведем с ее помощью \(49_{16}\)в двоичную систему счисления: из таблицы 4 – это 0100, а 9 – это 1001. Значит, \(49_{16}\)= 01001001. Разобьем это число на триады: то есть справа налево на тройки. Получим 001|001|001 (мы дополнили незначащим нулем число, чтобы в начале тоже получилась тройка).

Теперь переведем полученные тройки в восьмеричную систему счисления. Опять посмотрим на таблицу: в столбике триады видим, что 001 – это 1, значит, получаем 111. Итак, \(49_{16}\)= \(111_{8}.\)

2) Переведем число \(49_{16}\)в десятичную систему счисления. \(49_{16}=4*16^{1}+9*16^{0}=4*16+9=64+9=73.\)Теперь переведем \(73_{10}\)в восьмеричную систему счисления: можно делением на основание системы счисления, то есть 8,

а можно с помощью разложения на степени восьмерки: 73 = 1 \(\cdot\)\(8^2\)+ 1 \(\cdot\)\(8^1\)+ 1 \(\cdot\)\(8^0\)– тогда само число – это записанные подряд слева направа числа, на которые умножались степени восьмерки. Обоими способами получим, что \(73_{10}=111_{8}.\)

Ответ: 111

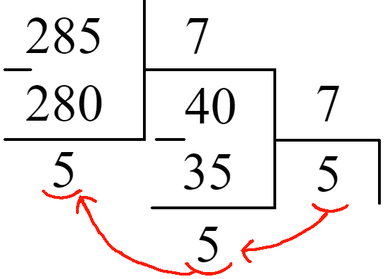
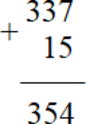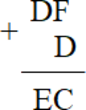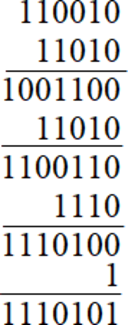Т.к. ответ нужно дать в десятиричной системе счисления, легче всего будет перевести оба числа в нее и сложить, но покажем и способ с переводом в шестнадцати- и восьмеричную системы и сложения в них.

1) Переведем \(DF_{16}\)и \(15_{8}\)в десятичную систему счисления.

\(DF_{16}=D*16+F=13*16+15=223, 15_{8}=1*8+5=8+5=13.\)Теперь сложим полученные числа: \(DF_{16}+15_{8}\)= 223 + 13 = 236.

2) С помощью таблицы тетрад и триад

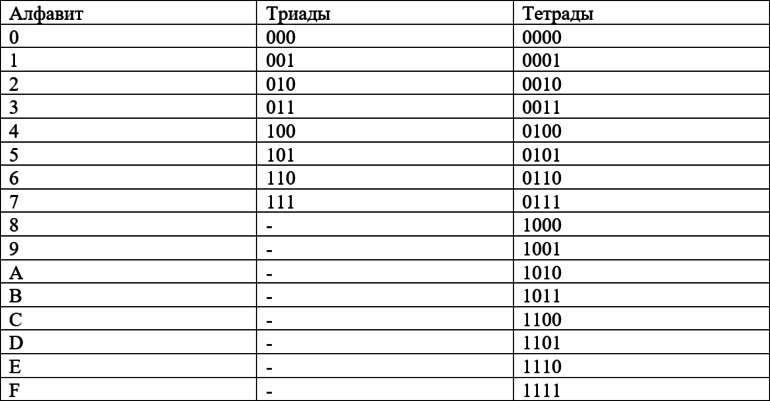
переведем \(DF_{16}\)в восьмеричную систему счисления:

По таблице определяем, что D – это 1101, F – 1111 (т.к. переводим из шестнадцатиричной, смотрим на столбик тетрады), то есть \(DF_{16}\)= 11011111 (получили число в двоичной системе). Теперь разделим его на триады справа налево, добавив незначащий ноль слева, чтобы получить триаду (оставалось только два символа): 011|011|111. Посмотрим на столбик триады: получается, 011 – это 3, 111 – это 7. Значит, \(DF_{16}\)= \(337_{8}.\)

Теперь сложим в восьмеричной системе \(337_{8}\)и \(15_{8}:\)

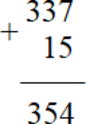
(Мы складываем поразрядно и берем остаток от деления на 8, при этом переносим ”десятки”’, как при обычном сложении в десятичной системе: 7 + 5 = 12 – остаток от деления на 8 = 4, 12 > 8 – добавляем единицу к более старшему разряду, 3 + 1 = 4 – но добавляем единицу из предыдущего разряда? а следующая тройка остается без изменений).

Теперь переведем 54 из восьмеричной системы в десятичную: \(354_{8}\)= \(3 \cdot 8^2 + 5 \cdot 8^1 + 4 \cdot 8^0\)= 236.

3) аналогично 2) переведем \(15_{8}\)в шестнадцатиричную систему (получим D – см. таблицу) и сложим с \(DF_{16}:\)

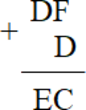
(Складываем поразрядно и берем остаток от деления на 16: F + D = 28, остаток от деления на 16 – 12, то есть C, лишнюю ”десятку” переносим в следующий разряд, то есть D становится E).

Переведем полученное в десятичную систему: \(EC_{16}\)= 14 * 16 + 12 * 16 = 236.

Ответ: 236

Можем решить задачу двумя способами: перевести все числа в двоичную систему и сложить или перевести в десятичную, сложить и результат перевести в двоичную.

1) Переведем все числа в двоичную систему:

Начнем с простого: \(1_{32}\)– так и будет один в любой системе счисления, в том числе и в двоичной.

Теперь посмотрим на таблицу триад и тетрад:

Видим, что \(32_{16}\)(смотрим на соответствующие строчки (3 и 2) в тетрадах, т.к. переводим из шестнадцатиричной) в двоичной системе – это 00110010.

\(32_{8}\)переведем с помощью триад (т.к. восьмеричная система) – смотря на соответствующие строки, получим 011010.

Теперь переведем \(32_{4}.\)В таблице этого нет, но по аналогии 3 в двоичной системе – это 11, а 2 – 10. Значит, получим 1110.

Итак, все числа переведены: получили 1, 110010, 11010, 1110. Теперь сложим их.

Теперь посчитаем количество единиц. Ответ – 5.

2) Переведем все числа в десятичную систему счисления.
\(32_{4} = 3 \cdot 4 + 2 = 12 + 2 = 14 \\32_{8} = 3 \cdot 8 + 2 = 24 + 2 = 26 \\32_{16} = 3 \cdot 16 + 2 = 48 + 2 = 50 \\1_{32}=1.\)

Теперь сложим все числа: 14 + 26 + 50 + 1 = 91. Переведем 91 в двоичную систему счисления с помощью степеней двойки: 91 = \(1 \cdot 2^6 + 0 \cdot 2^5 + 1 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0.\)Перепишем слева направо числа, на которые умножались степени двойки: 1011011 – это и есть 91 в двоичной системе счисления. Видим, что единиц здесь 5.

Ответ: 5

Переведем все числа в десятичную систему счисления: \(12_{3} = 1 \cdot 3 + 2 = 5, 2001_{5} = 2 \cdot 5^{3} + 1 = 2 \cdot 125 + 1 = 250 + 1 = 251\)– и сложим: 251 + 5 + 29 = 285. Далее переведем 285 в семеричную систему счисления: 1) можем делением 285 на 7, 2) можем разложением на степени 7. Получаем, что \(285 = 555_{7}.\)

1)

2) 285 = \(5 \cdot 7^2 + 5 \cdot 7^1 + 5 \cdot 7^0\)– значит, в семеричной системе получаем 555 (переписываем слева направо числа, на которые умножаем степени 7).

Ответ: 555

Переведем оба числа в десятичную систему счисления.

\(40_{6} = 4 \cdot 6 + 0 = 24 + 0 = 24,\)\(43_{5} = 4 \cdot 5 + 3 = 23.\)

\(24 > 23 \Rightarrow 40_{6} > 43_{5}.\)Разность этих чисел равна \(24 - 23 = 1.\)

Ответ: 1